你是不是也感觉——AI 越来越像人了？

它能理解你的问题、给你建议，甚至还能陪你聊天谈心；

大模型（LLM）不仅在说话，简直是在思考。

但你有没有想过：这些模型为什么像人类一样“思考”？

是因为数据多了？参数大了？算法复杂了？LLM背后的逻辑如果用一句话总结，应该是——LLM 背后其实是利用了一个 18 世纪的“人类思考公式”：贝叶斯定理（Bayes’ Theorem）。

贝叶斯定理是以18世纪英国数学家和神父托马斯·贝叶斯（Thomas Bayes）的名字命名的，是一种用于更新我们对某个事件发生概率的方法。通俗地理解，你可以将其比作一种“修正”或“调整”我们的信念。

假设你有一个关于某件事情发生概率的初始猜测，这个猜测可能是主观的、基于经验的、或者是先验知识。然后，当你获得新的信息或证据时，你可以使用贝叶斯定理来重新评估你的初始猜测，得到一个更准确的估计。

每次我们面对不确定的事物做出决策时——一直以来我们都是这样做的——都可以利用贝叶斯定理来判断该决策在多大程度上算是个好决策。

事实上，无论是怎样的决策过程，无论你为了实现某个目标对世界产生了多大的影响，无论你掌握的信息多么有限，无论你是正在寻找高浓度葡萄糖环境的细菌，是正在利用复制行为传播遗传信息的基因，还是正在努力实现经济增长的政府，只要你想把事情干好，你就离不开贝叶斯定理。

AI（人工智能）本质上也是贝叶斯定理的一个具体应用。

从最基本的层面来说，AI 所做的事情就是“预测”。一个可以分辨猫狗图像的 AI 应用，本质上就是在根据过往的训练数据和当前的图像信息去“预测”人类对图片的判断。DALL-E 2、GPT-4、Midjourney 等各种优秀的 AI 应用，正在以令人应接不暇的速度一次次冲击人们的认知。

不过，这些和你谈笑风生、为你生成高质量图像的 AI，本质上也是在做预测，只不过它们预测的是人类作家、人类艺术家面对这些提示词时会如何作答。这些预测行为的基础都是贝叶斯定理。

AI 本质上是在不确定的情况下做出抉择。谷歌的密码学家保罗·克劳利告诉我：“如果你懂贝叶斯理论，你就会发现 AI 在最基本的层面上用到了大量贝叶斯思想。”

现代的那些 AI 神经网络存在大量节点，这些节点就像大脑中的神经元一样。AI 会在学习过程中为不同的节点链接赋予不同的权重，从而加强或削弱各节点之间的关联程度。

保罗·克劳利表示：“AI 内部有一套评分机制，权重体系越复杂，它的得分就越低，反之就越高。如此一来，我们就能迫使它尽量采用更简单的假说，而不是更复杂的假说，这看上去完全就是贝叶斯思想；其先验概率就是建立在奥卡姆剃刀原则之上的。进行完整的贝叶斯计算需要耗费大量算力，所以现代这些 AI会尽量使用算力需求较低但性能表现并不会逊色多少的简化算法。”

不管怎么说，贝叶斯思想都是 AI 的基本原理之一。“大多数现代AI 系统的基本思想都是贝叶斯定理，因为它们关心的都是不确定情况下的推理方法”。

事实上，有一种 AI 算法就叫“贝叶斯机器学习”，它的整个构架都在模仿贝叶斯定理。

假定现在有一个非常简单的 AI，它的任务是识别老鼠、狗、狮子的图片。如果是十几年前，这种 AI 足以令人感到震撼，但放到今天来看，它简直太普通了（其实就在 2017 年，我为第一本书的创作而四处走访时，AI 能够将猫狗区分开来还是一件非常新奇的事。至于现在，你只需要掏出自己的智能手机就可以做到这一点，它甚至可以在几分之一秒内将照片库中的狗狗、婴儿、海滩等类别的照片全部给你筛选出来）。

理论上来说，它的工作方式是这样的：

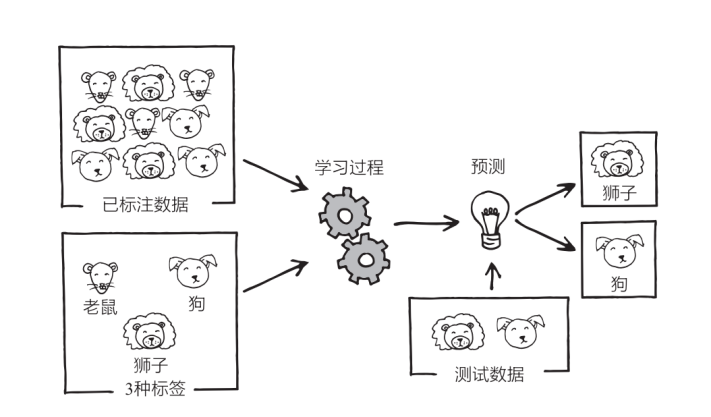
你“喂”给 AI 几百万或几千万张分别标好“老鼠”“狗”“狮子”的图片，让它利用这些“已标注数据”进行训练，然后它就会以某种方式反复学习数据。学习完成之后，你需要再拿几张它没见过的图片（“测试数据”）进行测试，此时它会根据自己的学习经验对这些测试图片做出最佳猜测，并给这些图片分别标上“老鼠”“狗“狮子”的标签。

AI 的这种学习方式就是所谓的“监督学习”。它所干的事情，就是预测“那些喂给自己学习数据的人类”会给新图片标上什么标签。”

当然，我们也可以用贝叶斯思想去解释这一过程，二者几乎是一样的：在看到某张图片之前，这个 AI 可能会主观地认为这是一只狮子的先验概率为 1/3，即 p ≈0.33。看到图片之后，也就是得到新信息之后，它会将这一概率更新为 p=0.99，或其他什么数字。先验概率、似然比、后验概率。

我们可以更具体一些。现在我们将情况进一步简化，把上面的例子看成一张图，图上面有一堆数据点。此时 AI 的任务是分析图像，然后找到一条能够穿越这些数据点的最佳拟合直线。事实上，我们根本不需要强大的 AI 来干这种事，因为这只是线性回归而已，高尔顿那个年代的统计学家就可以轻松解决这一问题。不过原理是一样的。

假定这些数据点表示的是人们的鞋码与身高——你随机抽取了一大群人，测量了它们的身高和鞋码。图上 X 轴表示的是鞋码，Y轴表示的是身高。通常来说，这些数据点会分布在左下至右上的区域附近。

AI 的任务就是找出这些数据点的最佳拟合直线。当然，你也可以凭感觉来画，但我们最好采用一个已经相当成熟的方法，即最小二乘法。在图上画一条直线，然后测量每个数据点和这条直线的垂直距离，这一距离就是“误差”。将每个点的距离，也就是误差，取平方值（平方是为了让所有数都是正数），然后将所有平方值加总，得到平方和。

我们的目标就是找到能让平方和达到最小值的直线，即每个数据点的平均距离最短的直线。

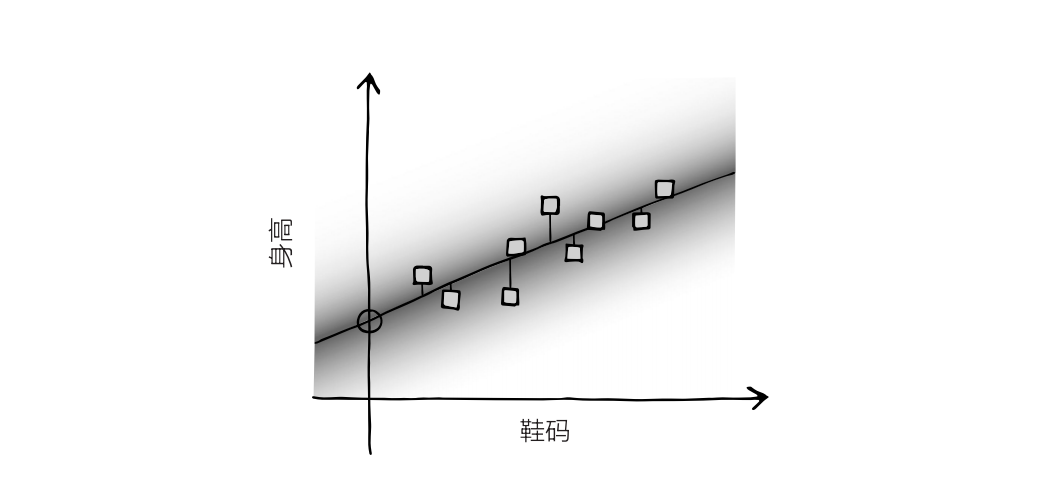
这些数据点可以视为 AI 的训练数据，而这一过程也用到了贝叶斯思想。首先，图上分布着一条直线，代表着宽泛的先验概率。然后我们在图上加入了数据点——代表数据。之后这条直线会根据数据而移动，得出后验分布。最后这条直线又会成为下一批数据的先验分布。

假如你现在知道一个人的鞋码是 11 号，想用它预测这个人的身高，那它就会用最小二乘法画出一条最佳拟合直线，然后读取横坐标 11 所对应的纵坐标，这个纵坐标就是 AI 对身高的最佳猜测。它有多大把握，取决于训练数据有多少，以及训练数据有多分散。数据越分散，把握就越小。

当然，这只是 AI 最基本的原理，实际上它们要比这复杂得多，涉及的参数也不会只有鞋码、身高，而是成千上万个，但基本思路是一样的。所有 AI 都需要大量的训练数据，然后根据某些参数去预测另一些参数的值。

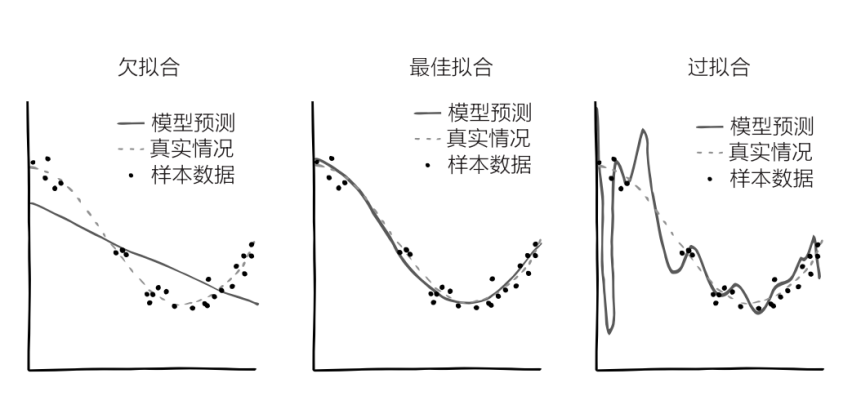
目前为止，我们一直假设这条线是直线，其实真实情况下它更可能是曲线。如果 Y 轴表示的是“新冠病毒感染者的全球病例数”，X 轴表示的是“时间”，起始时间是 2019 年 11 月，那么最符合实际情况的应当是条指数曲线，因为病例数量每隔几天就会翻一番。有的时候，最佳拟合曲线会长得像英文字母 S 或 J，也可能是一条正弦曲线，或其他什么形状的曲线。当然你可以让 AI 一直依照直线去模拟，但大多数情况下这并不是一个好的选择：这会导致这条线“欠拟合”。

同样，你也可以让 AI 变得极为复杂，这样它就会画出一条七扭八歪的、完美穿过每一个数据点的曲线，此时误差的平方和等于0。虽然看起来很美好，但这很可能无法反映出数据背后的真实情况。出现新数据时，这条七扭八歪的曲线很可能距离新的数据点相去甚远，因为这条线已经变得“过拟合”了。

由此可见，问题的关键在于 AI 应当在多大程度上去拟合曲线，这种程度就是自由度。自由度有点像前两节中的“超参数”——除了最佳拟合曲线这个问题，我们还应当关心一个更高层次的问题，即这条曲线应当有多“扭曲”。AI 对这些参数的先验判断就是它的超先验。通常情况下，在其他情况都相同的情况下，AI 会在两条线中选取更简单的那条。还记得吗？在讲奥卡姆剃刀原则的时候我们曾提到，我们要权衡假说的简单程度和符合程度，AI 也需要做这种权衡。

医用 AI 在试图分辨癌症的扫描结果时，ChatGPT 在试图仿照《英王钦定本圣经》中描写的一个男人努力取出电视机里的三明治的情节时，都用到了贝叶斯思想。它们都在根据训练数据生成先验概率，然后用这些先验概率预测未来的数据。

虽然贝叶斯定理不是万物理论，但实际上也差不多了。一旦你开始站在贝叶斯定理的视角去看待问题，你就会发现贝叶斯定理真的是无处不在。